Apresentação Cálculo
Introdução
As aplicações do Cálculo em geral se encaixam em três grandes grupos:
- Limites;
- Taxas de variações (derivadas);
- E cálculo de áreas (integrais).
Nesta aula vamos começar tratando da questão do cálculo de áreas e a sua relevância do ponto de vista de aplicações. Depois, abodaremos o problema da reta tangente a uma curva.
O Cálculo (seja de limites, derivadas ou até mesmo de integrais) está presente em diversas áreas do conhecimento, sendo algumas delas as seguintes:
- Física;
- Engenharia;
- Economia (sou “cético” em muitas aplicações, mas é usado).
Movimento Uniformemente Variado: porque o cálculo de áreas é útil
Considerar uma partícula descrevendo uma trajetória ao longo de uma reta, em um movimento uniformemente variado (isto é, a aceleração é constante).
É certo que você pode encontrar outras abordagens para o mesmo problema, mas todos eles vão exigir algum conjunto de suposições para o mesmo. No nosso caso, vamos partir do princípio que a aceleração é a taxa de variação da velocidade em função do tempo. Sendo a aceleração constante (por suposição), ela pode ser expressa da seguinte maneira:
$$ a = \frac{\Delta v}{\Delta t}, $$
sendo que essa relação é constante ao longo do tempo. Dessa forma, considerando variação da velocidade inicial, denotada por $v_0$, até a velocidade no instante $t$, temos (considere $t=0$ o instante inicial):
$$ a = \frac{v(t) - v(0)}{t - 0} = \frac{v(t) - v_0}{t}, $$
donde segue que $v(t) = v_0 + a t$, sendo $a$ e $v_0$ constantes. Para facilitar a visualização, vamos assumir que tais constantes são positivas.
Colocando em um gráfico Velocidade v.s. Tempo, o gráfico desta trajetória seria da seguinte forma:
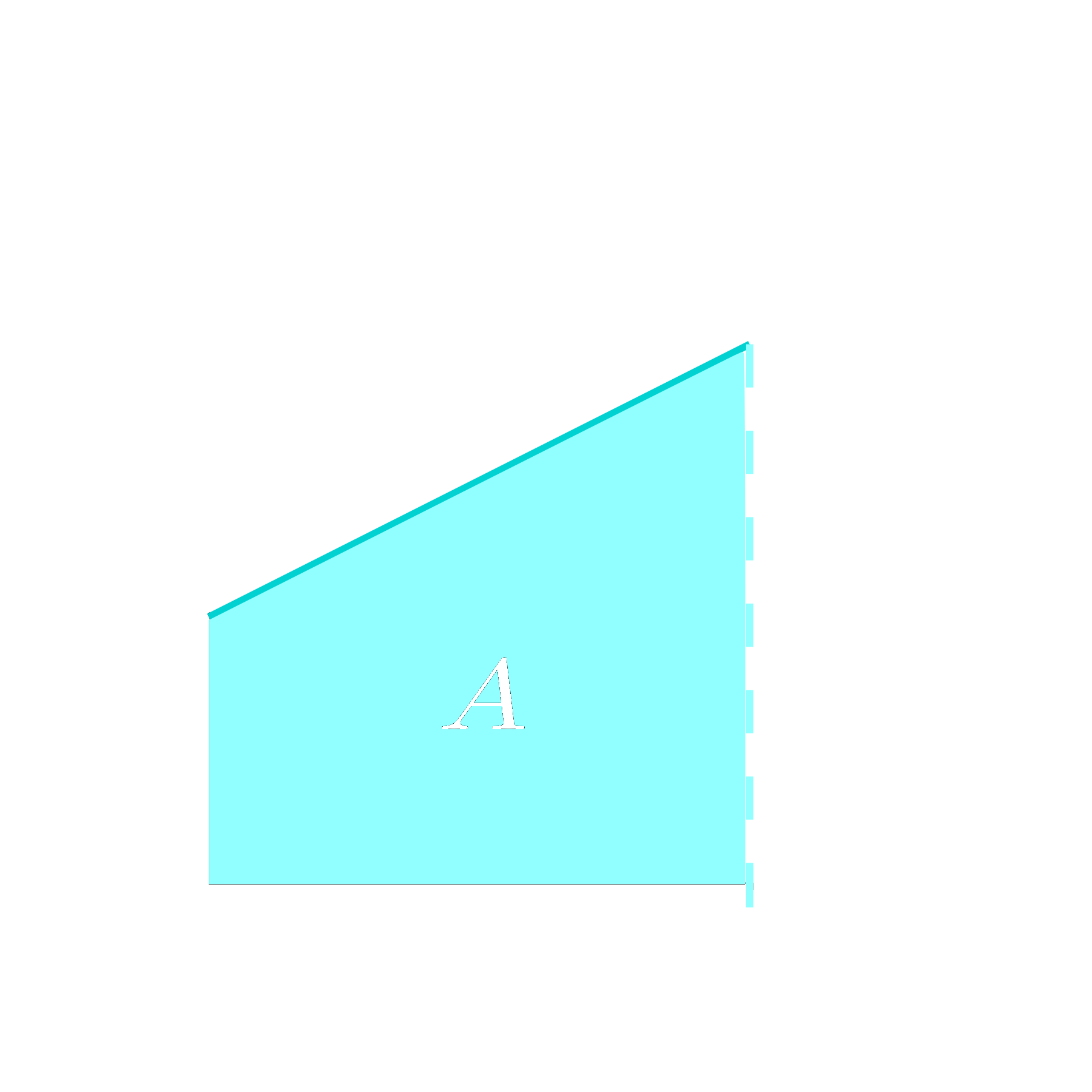
O nosso objetivo é o seguinte: à partir do gráfico, calcular o deslocamento da partícula. A notícia boa é que o deslocamento está associado à área $\textbf{A}$ conforme indicado na figura.
Note que a figura formada é simples: um trapézio. Vamos um pouco além: suponha que você não saiba calcular área de trapézios… apenas de retângulos e triângulos. Uma estratégia possível seria quebrar o trapézio em um retângulo e um triângulo. As dimensões destas figuras estão apontadas na ilustração a seguir:
Desta forma,
$$ A = A_1+A_2 = \frac{1}{2}(v(t)-v_0)t+v_0t = v_0 t+\frac{1}{2}at^2.$$
Como $A$ é o deslocamento, $A = \Delta S = S(t) - S(0) = S(t) - S_0$, daí concluímos a famosa fórmula para o deslocamento da partícula
$$ S(t) = S_0 + v_0 t+\frac{1}{2}at^2.$$
Vamos resumir o que foi feito até aqui:
-
Partimos da hipótese de que a aceleração é a taxa de variação da velocidade em função do tempo, e que esta aceleração é constante, obtend a relação $v(t) = v_0 + a t$;
-
Assumimos também que o deslocamento entre o instante $t$ e o início da trajetória é a área em baixo do gráfico da função de $v(t)$;
-
Assim, derivamos a fórmula $S(t) = S_0 + v_0 t+\frac{1}{2}at^2$.
O ponto principal é o seguinte: o cálculo de área é capaz de relacionar grandezas físicas, sendo útil para derivar fórmulas. No nosso exemplo, em especial, conhecendo-se a função da velocidade em função do tempo, é possível calcular o deslocamento.
É possível que a fórmula $S(t) = S_0 + v_0 t+\frac{1}{2}at^2$ seja do teu conhecimento. Agora vem o que talvez você não saiba: para uma partícula deslocando-se na reta, com velocidade $v(t)$, o deslocamento é exatamente a área do gráfico formado por $v(t)$, do instante $t=0$ até $t$. Para uma velocidade $v(t)$ que tem um gráfico “contínuo”, isto é verdade independente do gráfico formado por $v(t)$.
Isso quer dizer que se a expressão para $v(t)$ fosse diferente, você poderia calcular $S(t)$ através do cálculo de área.
Caso mais geral
O exemplo anterior naturalmente no compele ao caso mais geral. Considere que $f$ não tem saltos ou que o gráfico de $f$ pode ser traçado sem tirar a caneta do papel (intuitivamente falando é o que nos chamamos de continuidade).

Agora temos que abordar um novo problema: como calcular, de forma geral, áreas abaixo de gráfico de funções, como ilustrado na figura anterior?
Para responder esta pergunta, vamos remontar a uma técnica que remonta à Gŕecia Antiga: o método da exaustão.
Técnica da exaustão
Considere o círculo de raio $R$, conforme a figura:

Sabemos hoje que o círculo possuí área $A = \pi R^2$. Para calcular a área, os gregos sabiam que a proporção entre a área e o diamêtro ao quadrado era constante, isto é:
$$\frac{A}{D^2} = c.$$
OBS: Atualmente sabemos que $\displaystyle \frac{A}{D^2} = \frac{\pi R^2}{4 R^2} = \frac{\pi}{4}.$
Dessa forma, na grécia antiga o cálculo foi feito considerando o círculo de raio unitário. A ideia consistiu em fazer aproximações sucessivas com áreas que os gregos sabiam calcular; No caso, polígonos regulares inscritos e circunscritos.
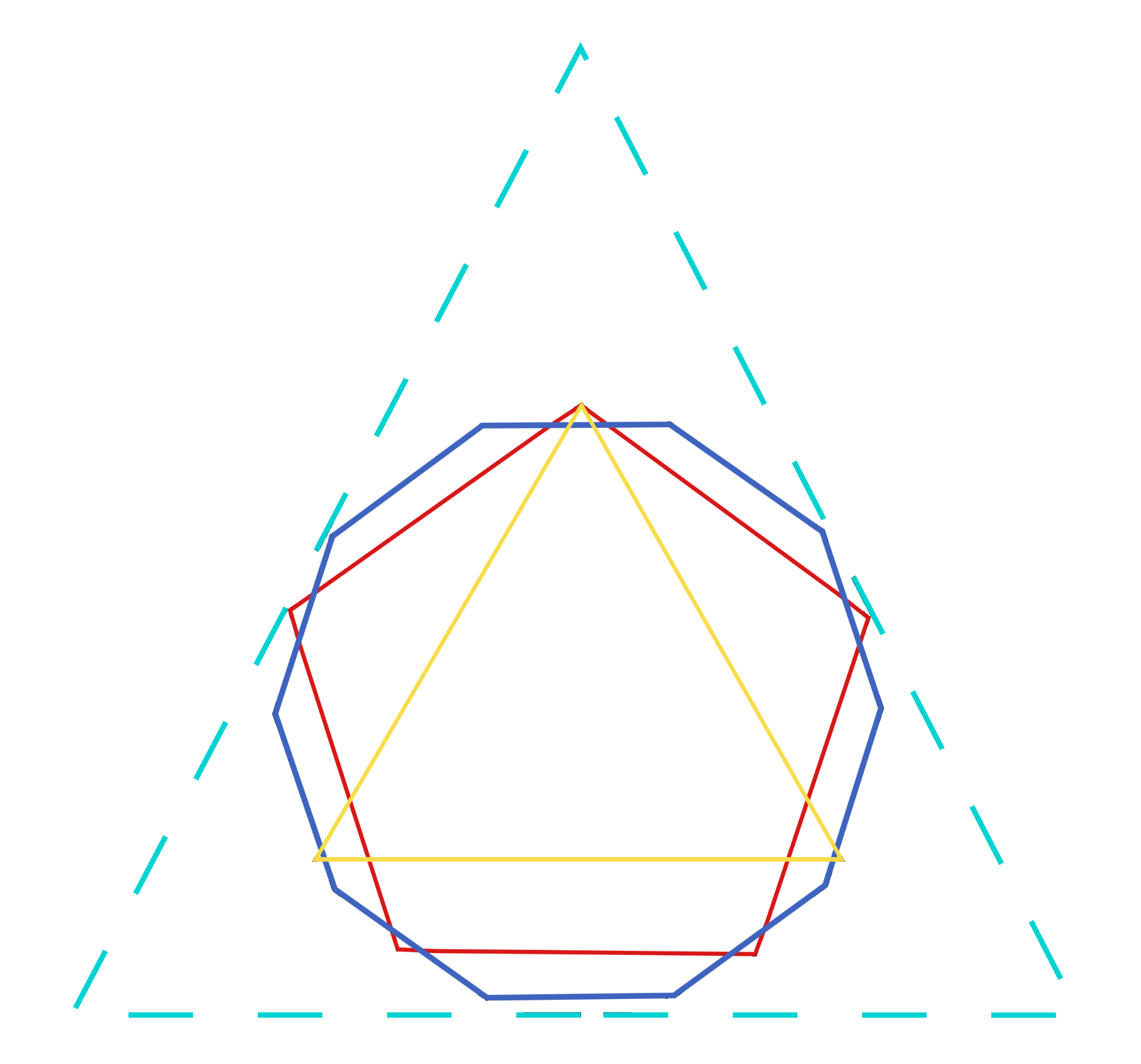
Conforme você pode observar, quanto mais lados o polígono inscrito tem, mais próximo estamos do círculo. Desta forma, a área dos polígonos inscritos, em função do número de lados, é uma sequência que se aproxima, por valores menores, da área $A$. Analogamento, a área dos polígonos circunscritos, em função do número de lados, é uma sequência de áreas que se aproximam, por valores maiores, de $A$. Assim, estabeleceu-se a seguinte estimativa:
$$\frac{223}{71}< A_{1} <\frac{22}{7},$$
em que $A_{1}$ é a área do círculo de raio 1. Observe que de forma indireta isto é exatamente o cálculo do valor de $\pi$ uma vez que $A_1 = \pi 1^2 = \pi$ (mas a princípio os gregos não sabiam exatamente o que seria o $\pi$).
Voltando a proporção entre área a diâmetro ao quadrado, é forçoso observar que o cálculo de diâmetro é, por definição, conhecido , isto é $D = 2R$, no caso do círculo de raio 1 o diâmetro é 2. Assim, temos o seguinte:
$$c = \frac{A_1}{D^2} = \frac{A_1}{4},$$
isto é, $A_1 = 4c$. Assim, para a área do círculo de raio $R$, temos
$$A = c D^2 = 4 c R^2 = A_1 R^2,$$
de forma que uma aproximação para $A_1$ implica em saber aproximar, para qualquer $R$, a área do círculo de raio $R$. Posteriormente, a área de $A_1$ ficou conhecida como o que entendemos hoje como sendo $\pi$. Em resumo:
- O cálculo da área do círculo de raio $R$ foi reduzido ao problema de calcular a área de raio 1;
- O cálculo do círculo unitário foi aproximado mediante exaustão, aproximando-o por polígonos inscritos e circunscritos.
A ideia central aqui é a seguinte: Dividimos o nosso problema de área em problemas de áreas menores e aproximados de forma que, através de uma sequência de cálculo de áreas conhecidas, é possível cada vez mais se aproximar do cálculo da área desejada.
Faremos algo análogo:
- “Quebrar” uma figura em figuras menores cujo cálculo de área seja simples ou conhecido;
- Repetir o processo anterior até que as figuras menores estejam “próximas o suficiente” da figura maior.
Assim, considerando novamente a figura,

faremos o seguinte: vamos aproximar a área abaixo da função $f$ por retângulos.
Para construção a seguir fazer sentido geometricamente, é importante inicialmente considerarmos $f$ uma função positiva no intervalo $[a,b]$.
Começamos tomando retângulos com largura uniformoe $\Delta x = \frac{b-a}{n},$ na qual $n$ é o número de retângulos. Para ser mais específico,
- Particionamos o intervalo [a, b] em $n + 1$ pontos:
- $x_0 = a$,
- $x_1 = x_0 + \Delta x = a + \Delta x$,
- $x_2 = x_1 + \Delta x = a + 2 \Delta x,$
- $\vdots$
- $x_{n+1} = \dots = a + n \Delta x = b.$
- O retângulo $i$ tem como base $[x_{i-1}, x_{i}]$ e altura é exatamente $f(x_i^{*})$ para algum $x_i^{*} \in [x_{i-1}, x_{i}]$.
- Portanto, cada retângulo tem área
$$A_i = f(x_i^{*}) \Delta x.$$
Pegando $x_i^{*}$ de forma que $f(x_i^{*})$ é o menor possível em $[x_{i-1}, x_{i}]$, teríamos um gráfico como a seguir:
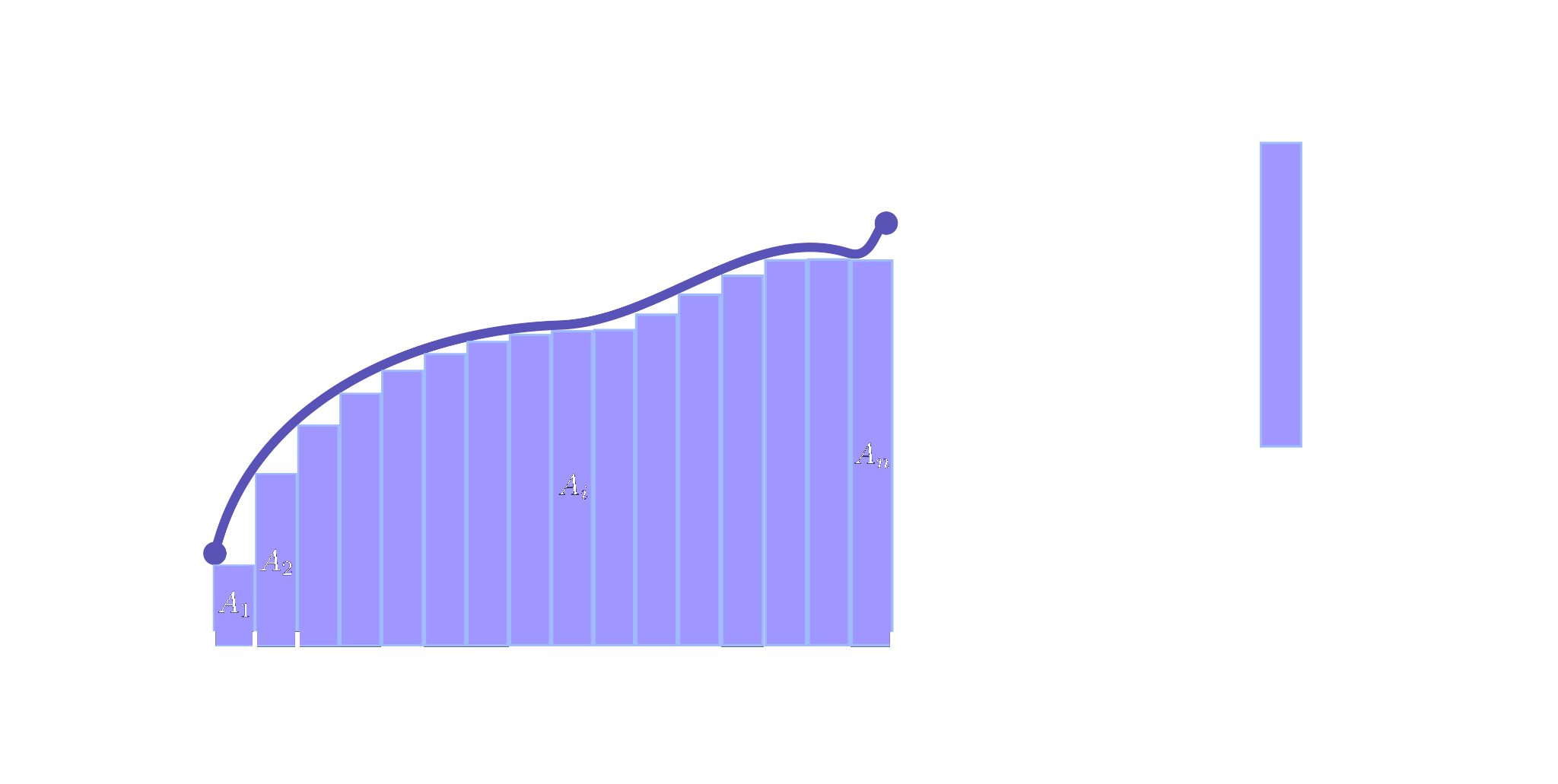
Ao final, a aproximação para a área desejada é o seguinte:
$$A \approx \sum_{i=1}^{n} f(x_i^{*}) \Delta x.$$
Note que essa aproximação é tão melhor quanto mais retângulos sejam utilizados para aproximar a área. Quando $n$ é suficientemente grande, a aproximação estará suficiente próxima da área desejada.
Na linguagem da grécia antiga, faríamos a aproximação através do que era chamado de “exaustão”. Em termos modernos, aplicamos o que chamamos de limite. E, conforme será visto em aulas futuras, o cálculo da área neste caso é exatamente a integral da função $f$ no intervalo $[a, b]$, denotada por $\displaystyle \int_a^b f(x) dx$. Em outras palavras,
$$\int_a^b f(x) dx = \lim_{n\rightarrow\infty}\sum_{i=1}^n f(x_i^*)\Delta x.$$
Derivada e o problema da tangente
Tangente vem do latin tangens, que significa “tocando” em latim. A definição de Euclides para a circunferência é o seguinte: é a reta que passa em um único ponto. Essa definição para figuras mais gerais é, infelizmente, inapropriada. Intuitivamente o que queremos é uma reta “que passa raspando” na curva, tocando num ponto em específico. Mas esta reta pode cruzar outros pontos da curva, conforme ilustrado na figura a seguir:

Para elaborar o conceito em termos modernos, considere a seguinte curva dada por $y = f(x)$, considere os pontos $P = (a, f(a))$ e $Q = (x, f(x))$. Começamos trançando a reta que passa pelos pontos $P$ e $Q$ (nota: esta reta chamamos de reta secante). Assim, consideramos o ângulo $\theta$ do triângulo retângulo formado, conforme indicado na figura:
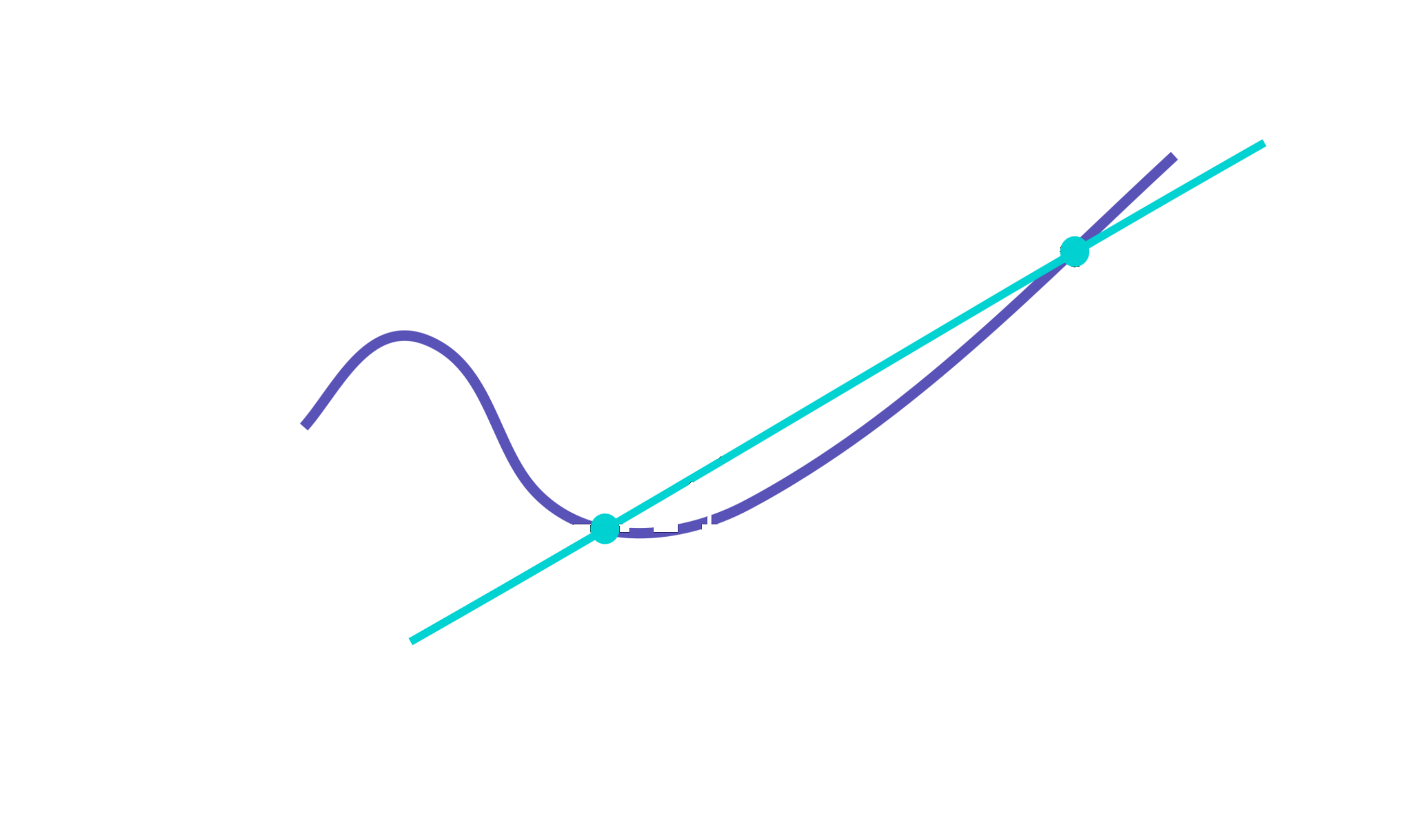
Observe que a inclinação da reta secante é a tangente de theta:
$$m_{PQ} = tan(\theta) = \frac{f(x) - f(a)}{x - a}.$$
Podemos fazer o ponto $Q$ cada vez mais se aproximar de $P$,

isto no fundo é equivalente a fazer $x$ se aproximar $a$. Se fizermos isso, exaustivamente, a reta secante vai cada vez mais se aproximar duma reta que passa “raspando” ao ponto $P = (a, f(a))$. Quando essa aproximação sucessiva for possível, diremos que “o limite” dessa aproximação é exatamente o coeficiente angular (inclinação) da reta tangente buscada.
Definição: A reta tangente a uma curva $y = f(x)$ em um ponto $P(a,f(a))$ é a reta que passa por $P$ e que tem a inclinação $m = \displaystyle \frac{\Delta f}{\Delta x} \Bigr \rvert_{x=a}$ com $\Delta x \rightarrow a$ (se existir tal $m$).
Em termos de limites, $$m=\lim_{x\rightarrow a} \frac{f(x)-f(a)}{x-a},$$
se este limite existir.
Veremos ainda que $m=f’(a)$, isto é, a inclinação da reta tangente à $P(a,f(a))$, se existir, é chamado de derivada da função $f$ calculada em $a$.
Observação: Note que $x-a$ com $x\rightarrow a$ é equivalente a $h:= x-a$ com $h\rightarrow 0$ $$\lim_{x\rightarrow a} \frac{f(x)-f(a)}{x-a} = \lim_{h\rightarrow 0} \frac{f(a+h)-f(h)}{h}.$$
O conceito de derivada é, essencialmente, a inclinação da reta tangente que passa pelo ponto:
Definição: A derivada de uma função $f$ no ponto $a$, denotada por $f’(a)$, é o limite
$$f’(a) = \lim_{h\rightarrow 0} \frac{f(a+h)-f(h)}{h},$$
quando este limite existir.
Note que a inclinação da reta tangente passando por $(a,f(a))$ é exatamente, quando existir, a derivada da função $f$ calculada em $a$.
Exemplo: Vamos calcular a equação da reta tangente a curva $y = x^2$ passando pelo ponto $(2, 4)$.
O ponto em questão é $P(2, 4)$ e um ponto levemente deslocado (e que ainda esteja sobre a curva $y = x^2$) seria $Q(2 + h, (2 +h)^2)$. Assim, o coeficiente angular da reta secante é
$$m_{PQ} = \frac{(2+h)^2 - 4}{h} = \frac{h^2 + 4h}{h} = h + 4.$$
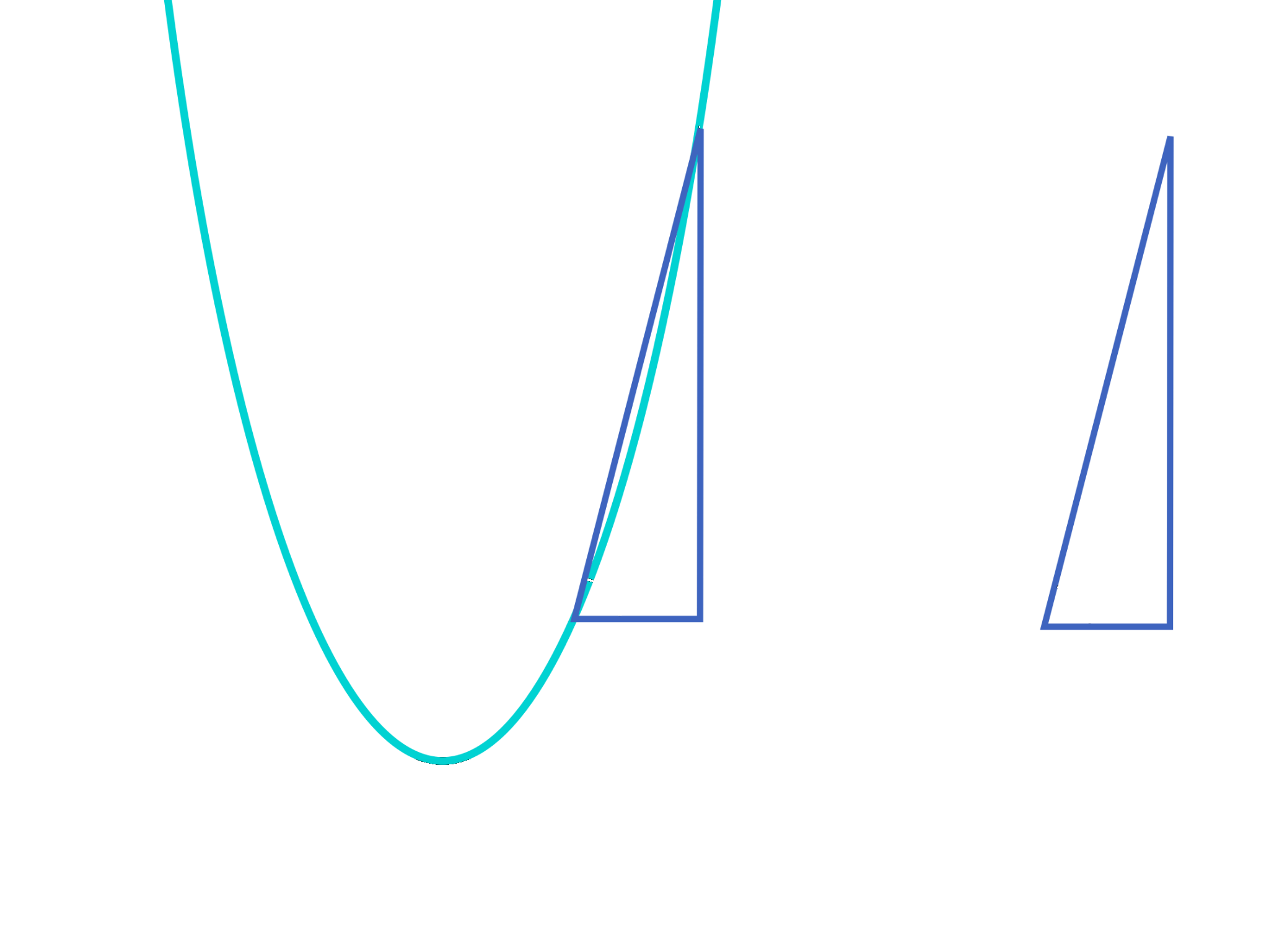
Observe que quando $h$ se aproxima de zero, $m$ tende a 4.
Dessa forma,
$$m = \lim_{h \to 0} \frac{(2+h)^2 - 4}{h} = \lim_{h \to 0} \frac{h^2 + 4h}{h} = \lim_{h \to 0} h + 4 = 4.$$
Por fim, usando a famosa fórmula
$$y - y_0 = m (x - x_0)$$
podemos obter a equação da reta tangente, uma vez que $m = 4$, $x_0 = 2$ e $y_0 = 4$, segue:
$$y - 4 = 4 (x - 2) = 4x - 8.$$
Isto é,
$$y = 4x - 4.$$
